4.4. Moviment
Segur que recordareu que, tal com ja hem vist, la funció draw() es repeteix 60 cops per segon. I també que ja hem comentat que això es pot canviar. La funció que ens permet canviar el nombre de vegades que es repeteix la funció draw() per segon es diu frameRate(). Podem fer servir aquesta funció de dues maneres diferents:
- Podem fer-la servir per a consultar quants cops per segon es repeteix actualment la funció draw().
- També podem fer-la servir per a fixar aquest valor.
Frame rate o fotogrames per segon, que és la traducció més habitual, és un concepte que ve del vídeo i es refereix al nombre de imatges que projecta un reproductor de vídeo en un segon. És un concepte heretat de les pel·lícules analògiques, però que es continua fent servir en el vídeo i animacions digitals. Al cinema, per a garantir la continuïtat de la imatge, es fan servir 24 fotogrames per segon.
L’exemple 8-1 del llibre fa servir la primera opció: consulta el frameRate() i mostra el resultat de la consulta a la consola. Si el feu servir, veureu que no sempre dona el mateix resultat, que va variant entre 55 i 65 aproximadament.
Fotogrames a p5.js
p5.js intenta que el nombre de fotogrames per segon sigui 60. Però això depèn de moltes coses: la velocitat del processador, de tot allò que s’estigui executant a l’ordinador, del navegador (no tots els navegadors executen JavaScript de la mateixa manera), del codi que hi hagi dins de draw(). p5.js s’ha de «barallar» amb totes aquestes possibilitats per a aconseguir que el nombre de fotogrames sigui l’indicat i es mantingui estable. Això és força complicat, per la qual cosa el valor fluctua.
L’exemple 8-2 afegeix la segona opció a la funció setup() i ens suggereix canviar el valor dels fotogrames per segon a nombres més baixos. Feu-ho i comproveu com es comporta a diferents velocitats.
Velocitat i direcció
Les nostres animacions tindran diferents objectes que es poden moure a diferents velocitats, de manera que tenint el nombre de fotogrames per segon de base, haurem de fer servir variables per a determinar la velocitat de cada objecte. Una cosa semblant passarà amb la direcció en què es mouen els objectes.
L’exemple 8-3 és un bon exemple de moviment fluid on fem servir una variable, speed, per a determinar la velocitat de l’objecte. Modificant el valor d’aquesta variable, l’objecte es mou més ràpid o més a poc a poc (proveu a modificar el valor d’speed a 1 i a 0.25).
El moviment va d’esquerra a dreta gràcies a la modificació de la variable x que ens marca la posició horitzontal. Quan l’x té un valor superior al límit dret del canvas, l’objecte es deixa de veure.
Un darrer detall interessant, malgrat ja ho hem vist, és el fet que pintant el fons de nou cada cop, esborrem la figura ja dibuixada abans de dibuixar-ne una de nova.
A partir d’aquest exemple bàsic, es poden fer diverses variacions. Així l’exemple 8-4 fa que quan la variable x té un valor més gran que la mida horitzontal del canvas més el radi de la figura (això vol dir que la figura haurà desaparegut), li posa el valor inicial perquè torni a sortir per la dreta. Aquesta variació es fa amb aquest codi:
if (x > width+radius) { // Si la imatge surt del canvas
x = -radius; // la movem a l’esquerra.
}
I l’exemple 8-5 fa que reboti quan arriba al final. Com podeu veure, el rebot implica dues coses: primer canviar la direcció (que no és més que fer la velocitat negativa) i, després, canviar la figura perquè la boca apunti a la dreta.
x += speed * direction; // Si direction és 1 es mou d’esquerra
// a dreta.
// Si direction és -1 es mou de dreta
// a esquerra.
if ((x > width - radius) || (x < radius)) {
direction = -direction; // Canviar la direcció
}
if (direction == 1) {
arc(x, 60, radius, radius, 0.52, 5.76); // Cap a la dreta
} else {
arc(x, 60, radius, radius, 3.67, 8.9); // Cap a la esquerra
}
Movent-se en qualsevol direcció
Moure un objecte de dreta a esquerra és fàcil. En general, qualsevol moviment horitzontal o vertical serà fàcil de simular perquè només caldrà modificar la posició x o la posició y. Però si volem moure un objecte en una direcció que no sigui l’horitzontal o la vertical, caldrà modificar x i y de manera que el moviment sembli suau, per la qual cosa caldrà calcular quina posició haurà de tenir l’objecte en cada moment.
Aquest càlcul que ens permet dibuixar l’objecte on toca quan toca, rep el nom, en anglès, de tweening i, en català, li direm interpolar (posar una cosa entre altres).
Veient el codi de l’exemple 8-6 del llibre, ens pot semblar que la interpolació és una cosa complicada. Però no és així. Vegem l’exemple pas a pas per a veure que no és complicat.
Fe d’errades Al llibre hi ha una errada a la instrucció: Com que estem calculant la posició de l’y, startX hauria de ser en realitat startY i, per tant, la instrucció hauria de ser aquesta: Farem servir aquesta versió corregida en aquesta guia.y = startY + ((stopY-startX) * pct);
y = startY + ((stopY-startY) * pct);
El primer que fa l’exemple és declarar les variables que fa servir: vuit! Bé, fem un repàs de què fa cadascuna d’aquestes. Comencem per les quatre primeres que són les més fàcils d’entendre i indiquen la posició inicial i final de l’objecte:
var startX = 20; // Indica la posició x inicial var stopX = 160; // Indica la posició x final var startY = 30; // Indica la posició y inicial var stopY = 80; // Indica la posició y final
Les dues següents també són fàcils d’entendre: indiquen la posició actual de l’objecte:
var x = startX; // Posició x actual var y = startY; // Posició y actual
Només ens en queden dues que són una mica més complicades:
var step = 0.005; // Mida de cada pas que fem (de 0.0 fins a 1.0) var pct = 0.0; // Percentatge ja fet (0.0 to 1.0)
De les dues variables, pct és potser la més clara. Ens indica quin percentatge de recorregut ja hem fet. Començarem per 0 (per això sempre la inicialitzarem a 0.0) i acabarem quan sigui 1.0.
step és potser la variable més complicada d’entendre. Determina la mida de cada pas que farem i, a la pràctica, quants passos farem per anar d’un lloc a un altre. Si ens fixem en el codi que hi ha a la funció draw(), a cada volta el percentatge que hem avançat s’incrementa la quantitat guardada a la variable step.
Com que anem de 0 a 1 en increments de 0.005, això en realitat significa que farem 200 passos abans d’arribar al destí (0.005 * 200 ⇒ 1).
Vegem ara el codi de la funció draw():
function draw() {
background(0);
if (pct < 1.0) {
x = startX + ((stopX-startX) * pct); // nova posició x
y = startY + ((stopY-startY) * pct); // nova posició y
pct += step;
}
ellipse(x, y, 20, 20);
}
Fem una breu simulació de com funcionaria el programa.
Valors inicials:
var startX = 20; // Indica la posició x inicial var stopX = 160; // Indica la posició x final var startY = 30; // Indica la posició y inicial var stopY = 80; // Indica la posició y final var step = 0.005; // Mida de cada pas que fem (de 0.0 fins a 1.0) var pct = 0.0; // Percentatge ja fet (0.0 to 1.0)
| Núm. execucions draw() |
Valors de la variable pct quan entra en la funció draw() |
Valors de les variables x i y calculades dins l’ if x = startX + ((stopX-startX) * pct); y = startY + ((stopY-startY) * pct); |
|---|---|---|
| 1 | 0 | x = 20 + ((160 – 20) * 0) ⇒ 0 y = 30 + ((80 – 30) * 0) ⇒ 0 |
| 2 | 0.005 | x = 20 + ((160 – 20) * 0.005) ⇒ 20.7 (21) y = 30 + ((80 – 30) * 0.005) ⇒ 30.25 (30) |
| 3 | 0.010 | x = 20 + ((160 – 20) * 0.010) ⇒ 21.4 (21) y = 30 + ((80 – 30) * 0.010) ⇒ 30.5 (31) |
| 4 | 0.015 | x = 20 + ((160 – 20) * 0.015) ⇒ 22.1 (22) y = 30 + ((80 – 30) * 0.015) ⇒ 30.75 (31) |
Cada posició de l’xla calculem sumant a la posició inicial la distància a recórrer (posició final menys posició inicial) multiplicat pel percentatge que hem recorregut.
Com que treballem en píxels (i els píxels no es poden dividir) l’ordinador automàticament fa un arrodoniment, que és el valor que hem posat entre parèntesi al costat del resultat.
Exercicis
Per a entendre bé aquest exemple, val la pena provar de canviar algunes coses. Aquí hi ha unes quantes propostes:
- Canvieu l’origen i el final. Què passa quan l’x de l’origen (variable startX) és més gran que l’x de destinació (variable stopX)?
Per a entendre millor com funciona això dels passos, afegirem una variable més a què direm numeroP>. En aquesta variable guardarem el nombre de passos que volem fer des de l’inici fins al final. La declaració de les variables haurà de quedar d’aquesta manera:
var startX = 20; // Indica la posició x inicial var stopX = 160; // Indica la posició x final var startY = 30; // Indica la posició y inicial var stopY = 80; // Indica la posició y final var numeroP = 200; // Nombre de passos a fer entre els dos punts. var step = 1.0 / numeroP; // Mida de cada pas var pct = 0.0; // Percentatge ja fet (0.0 to 1.0)
Amb numeroP igual a 200 estem igual que a l’enunciat inicial (step tindrà el valor de 0.005). Canvieu el nombre de passos per a veure quins canvis es produeixen.
Moviment aleatori
Ja hem vist com la funció random() ens permet crear nombres aleatoris. Com vam veure, el primer paràmetre que li indiquem és el valor mínim i el segon el valor màxim. Amb la característica que el valor màxim no apareixerà mai. En matemàtiques ho expressem així: [min,max) (el mínim inclòs, el màxim exclòs).
Provem bé la funció random(). Proveu aquest codi (no necessitem la funció setup()):
function draw() {
var r = random(0, 10);
print(r);
}

Aquest és el resultat: ens escriu nombres aleatoris entre 0 i 10; 60 per segon. Són nombres amb molts decimals.
Fem un pas més, quedem-nos només amb la part entera:
function draw() {
var r = int(random(0, 10));
print(r);
}
Ara els nombres que ens dona són més comprensibles:
![]()
Fem un pas més, calculem el màxim i el mínim. Aquest codi us hauria de resultar fàcil d’entendre:
var maxim = 0;
var minim = 99;
function draw() {
var r = int(random(0, 10));
if (r > maxim) {
maxim = r;
print("Nou màxim: ",r);
}
if (r < minim) {
minim = r;
print("Nou mínim: ",r);
}
}
El que escriu aquest codi a la consola és alguna cosa semblant a això:
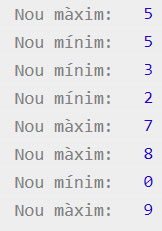
Podem provar amb diferents nombres de màxim i mínim per a veure com funciona.
Ara tenim prou clar com funciona la funció random(), per tant, podem provar l’exemple 8-7 del llibre. És molt semblant al nostre exemple, però posa com a màxim la posició x del ratolí.
L’exemple 8-8 és força interessant perquè genera un efecte molt efectiu. Vegem el codi i el comentem una mica:
function setup() {
createCanvas(240, 120);
}
function draw() {
background(204);
for (var x = 20; x < width; x += 20) {
var mx = mouseX / 10;
var offsetA = random(-mx, mx);
var offsetB = random(-mx, mx);
line(x + offsetA, 20, x - offsetB, 100);
}
}
El que fa aquest codi és, primer de tot, guardar a la variable mx el valor x de la posició del ratolí dividit per 10 (divideix per 10 perquè els canvis siguin més suaus). Proveu què passa si dividim per 2, per 100 o no dividim.
La posició del ratolí es fa servir per a crear totes les línies que càpiguen dins el canvas, però separades 20 píxels entre elles.
Quan pintem cada línia, a l’x de l’inici i a l’x del final les hi afegim o restem un valor calculat aleatòriament.
L’exemple 8-9 fa un pas més enllà i fa tot el moviment de manera aleatòria. Inicialment dibuixa el cercle al mig del canvas (independentment de la mida del canvas) i, després, el cercle es va movent depenent de dos valors (un per a x i un altre per a y) calculats aleatòriament.
Com sempre, és aconsellable provar l’exemple i canviar coses com ara la mida del canvas (per a comprovar que sempre es comença des del centre), la velocitat o el diàmetre del cercle.
Temporitzadors
p5.js compta el temps des de que s’inicia l’execució del nostre programa. Nosaltres podem consultar el temps transcorregut des de l’inici mitjançant la funció millis(). L’exemple 8-10 ens permet veure com va passant el temps. La funció millis() ens retorna el temps en mil·lisegons, el que vol dir que 1000 ⇒ 1 segon.
L’ús de la funció millis() ens permet fer que al nostre programa passin coses en un moment determinat. L’exemple 8-11 n’és un cas. A continuació, teniu un altre exemple que comentarem pas a pas. Bàsicament, és un cercle que es fa més gran cada segon, fins que arriba a un diàmetre de 200. A partir d’aquest moment, es va fent cada cop més petit, fins que arriba a un diàmetre de 0 i torna a créixer.
var diametre = 0;
var creix = true; // Variable que determina si el cercle ha de
// créixer o decréixer
function setup() {
createCanvas(480, 480);
}
function draw() {
var currentTime = millis(); // Guardem el temps actual
background(204);
if (currentTime % 1000 > 900) { // Calculem el residu de dividir
// per 1000
if (diametre == 200) { // Si arribem a 200 toca decréixer
creix = false;
}
if (diametre == 0) { // Si arribem a 0 tornar a créixer
creix = true;
}
if (creix) {
diametre++;
} else {
diametre--;
}
}
ellipse(width/2, height/2, diametre, diametre);
}
Aquest exemple és molt senzill i és fàcil de veure com funciona. L’única dificultat està en el fet de fer servir el residu de la divisió per 1000.
Moviment circular
Vegem com fer moure objectes pel canvas amb un moviment circular. Per a fer-ho, farem servir les funcions sin() i cos() que corresponen al sinus i al cosinus. Com que aquí no podem explicar trigonometria, ens haurem de conformar sabent que aquestes funcions retornen valors d’entre -1 i 1.
Aquí teniu un exemple que ens permet fer-nos una idea de com podem fer servir les funcions sinus i cosinus:
var x = 0.0;
function setup() {
createCanvas(400, 400);
strokeWeight(4);
}
function draw() {
stroke(0);
point(x*10,sin(x)*50+200);
stroke(255,0,0)
point(x*10,cos(x)*50+200);
x=x+0.08;
}
Aquest codi dona com a resultat aquest dibuix:
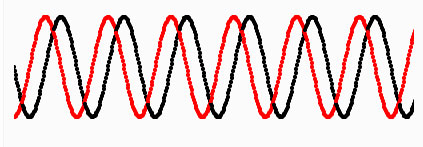
On la funció sinus s’ha dibuixat en negre i la cosinus en vermell.
Doncs bé, aquestes dues funcions es poden fer servir per a diverses coses. Per exemple, en l’exemple 8-12 es fa servir per a generar una sensació d’enfosquiment i aclariment del color del quadre. En aquest codi es fa servir la funció map() que, recordeu, ens permet fer un canvi d’escala d’un valor. Així, com que la funció sin() retorna un valor que va des de -1 fins a 1 i hem de tenir un nombre que vagi des de 0 (negre) fins a 255 (blanc), volem convertir el resultat de calcular el sinus en un color.
var sinval = sin(angle); print(sinval); var gray = map(sinval, -1, 1, 0, 255); background(gray);
L’exemple 8-13 ens mostra com es pot fer servir la funció sin() per a generar moviment.
Combinant la funció sin() i la funció cos() per a donar un valor a x i y, podem fer moviments circulars. L’exemple 8-14 aprofita aquesta possibilitat. Modifiquem i comentem l’exemple del llibre.
var angle = 0.0;
var offset = 120; // El centre del moviment circular.
// x = 120 i y = 120 és el centre del canvas.
var scalar = 50; // Un valor més gran dibuixa un cercle més gran
var speed = 0.05;
function setup() {
createCanvas(240, 240);
background(204);
}
function draw() {
var x = offset + cos(angle) * scalar;
var y = offset + sin(angle) * scalar;
ellipse(x, y, 40, 40);
angle += speed;
}
L’exemple 8-15 d’aquest capítol és el que no és complicat. Aquest dibuixa una espiral. El punt clau està en la variable scalar que canvia a cada volta i que multiplica el resultat del sinus i el cosinus.