4.4. Movimiento
Seguro que recordáis que habíamos visto ya que la función draw() se repite 60 veces por segundo. Y también que habíamos dicho que esto se puede cambiar. La función que nos permite cambiar el número de veces que se repite la función draw() por segundo se llama frameRate(). Podemos usar esta función de dos maneras diferentes:
- Podemos usarla para consultar cuántas veces por segundo se repite actualmente la función draw().
- También podemos usarla para fijar este valor.
Frame rate o fotogramas por segundo, que es la traducción más habitual, es un concepto que viene del vídeo y se refiere al número de imágenes que proyecta un reproductor de vídeo en un segundo. Es un concepto heredado de las películas analógicas, pero que se continúa usando en el vídeo y animaciones digitales. En el cine, para garantizar la continuidad de la imagen, se usan 24 fotogramas por segundo.
El ejemplo 8-1 del libro usa la primera opción; consultad el frameRate() y mostrad el resultado de la consulta en la consola. Si lo usáis, veréis que no siempre da el mismo resultado, que va variando entre 55 y 65 aproximadamente.
Fotogramas a p5.js
p5.js intenta que el número de fotogramas por segundo sean 60. Pero esto depende de muchas cosas: la velocidad del procesador, de todo aquello que se esté ejecutando en el ordenador, del navegador (no todos los navegadores ejecutan JavaScript del mismo modo), del código que haya dentro de draw(). p5.js tiene que «pelearse» con todas estas posibilidades para conseguir que el número de fotogramas sea el indicado y se mantenga estable. Esto es bastante complicado y por eso el valor fluctúa.
En el ejemplo 8-2 se añade, a la función setup() la segunda opción y nos sugiere cambiar el valor de fotogramas por segundo a números más bajos. Hacedlo y comprobad cómo se comporta a diferentes velocidades.
Velocidad y dirección
Nuestras animaciones tendrán diferentes objetos que se pueden mover a diferentes velocidades, de forma que teniendo el número de fotogramas por segundo de base, tendremos que usar variables para determinar la velocidad de cada objeto. Una cosa parecida pasará con la dirección en que se mueven los objetos.
El ejemplo 8-3 es un buen ejemplo de movimiento fluido donde usamos una variable, speed, para determinar la velocidad del objeto. Modificando el valor de esta variable, el objeto se mueve más rápido o más despacio (probad a modificar el valor de speed a 1 y a 0.25).
El movimiento va de izquierda a derecha gracias a la modificación de la variable x, que nos marca la posición horizontal. Cuando la x tiene un valor superior al límite derecho del canvas, el objeto se deja de ver.
Un último detalle interesante, a pesar de que ya lo habíamos visto, es el hecho de que pintando el fondo de nuevo cada vez, borramos la figura ya dibujada antes de dibujar una nueva.
A partir de este ejemplo básico, se pueden hacer variaciones. Así, el ejemplo 8-4 hace que, cuando la variable x tiene un valor más grande que la medida horizontal del canvas más el radio de la figura (esto quiere decir que la figura habrá desaparecido), le pone el valor inicial para que vuelva a salir por la derecha. Esta variación se hace con este código:
if (x > width+radius) { // Si la imagen sale del canvas
x = -radius; // la movemos a la izquierda.
}
Y el ejemplo 8-5 hace que rebote al llegar al final. Como podéis ver, el rebotar son dos cosas: primero, cambiar la dirección (que no es más que hacer la velocidad negativa) y, segundo, cambiar la figura para que la boca apunte a la derecha.
x += speed * direction; // Si direction es 1 se mueve de izquierda
// a derecha.
// Si direction es -1 se mueve de derecha
// a izquierda.
if ((x > width - radius) || (x < radius)) {
direction = -direction; // Cambiar la dirección
}
if (direction == 1) {
arc(x, 60, radius, radius, 0.52, 5.76); // Hacia la derecha
} else {
arc(x, 60, radius, radius, 3.67, 8.9); // Hacia la izquierda
}
Moviéndose en cualquier dirección
Mover un objeto de derecha a izquierda es fácil. En general, cualquier movimiento horizontal o vertical será fácil de simular porque solo habrá que modificar la posición x o la posición y. Pero si queremos mover un objeto en una dirección que no sea la horizontal o la vertical, habrá que modificar x e y de forma que el movimiento parezca suave, por lo que habrá que calcular qué posición tendrá que tener el objeto en cada momento.
Este cálculo que nos permite dibujar el objeto donde toca cuando toca recibe el nombre, en inglés, de tweening, y en castellano le llamamos interpolar (poner una cosa entre otras).
Viendo el código del ejemplo 8-6 del libro nos puede parecer que la interpolación es una cosa complicada. Pero no es así; vamos a ver el ejemplo paso a paso para ver que no es complicado.
Fe de erratas En el libro hay un error en la instrucción como estamos calculando la posición de la y, startX tendría que ser en realidad startY y, por lo tanto, la instrucción tendría que ser esta: Usaremos esta versión corregida en esta guía.y = startY + ((stopY-startX) * pct);
y = startY + ((stopY-startY) * pct);
Lo primero que hace el ejemplo es declarar las variables que usa: ¡ocho! Bien, vamos a hacer un repaso de qué hace cada una de ellas. Empezamos por las cuatro primeras, que son las más fáciles de entender; indican la posición inicial y final del objeto:
var startX = 20; // Indica la posición x inicial var stopX = 160; // Indica la posición x final var startY = 30; // Indica la posición y inicial var stopY = 80; // Indica la posición y final
Las dos siguientes también son fáciles de entender: indican la posición actual del objeto:
var x = startX; // Posición x actual var y = startY; // Posición y actual
Solo nos quedan dos que son algo más complicadas:
var step = 0.005; // Tamaño de cada paso que daremos (de 0.0 hasta 1.0) var pct = 0.0; // Porcentaje ya hecho (0.0 to 1.0)
De las dos variables, pct es quizás la más clara. Nos indica qué porcentaje de recorrido hemos hecho. Empezaremos por 0 (por eso, siempre la inicializaremos a 0.0) y acabaremos cuando sea 1.0.
step es la variable quizás más complicada de entender. Determina el tamaño de cada paso que daremos y, en la práctica, cuántos pasos haremos para ir de un lugar al otro. Si nos fijamos en el código que hay en la función draw(), en cada vuelta el porcentaje que hemos avanzado incrementa la cantidad guardada en la variable step.
Como vamos de 0 a 1 en incrementos de 0.005, en realidad esto significa que haremos 200 pasos antes de llegar al destino (0.005 * 200 ⇒ 1).
Vemos ahora el código de la función draw():
function draw() {
background(0);
if (pct < 1.0) {
x = startX + ((stopX-startX) * pct); // nueva posición x
y = startY + ((stopY-startY) * pct); // nueva posición y
pct += step;
}
ellipse(x, y, 20, 20);
}
Vamos a hacer una breve simulación de cómo funcionaría el programa:
Valores iniciales:
var startX = 20; // Indica la posición x inicial var stopX = 160; // Indica la posición x final var startY = 30; // Indica la posición y inicial var stopY = 80; // Indica la posición y final var step = 0.005; // Tamaño de cada paso que daremos (de 0.0 hasta 1.0) var pct = 0.0; // Porcentaje ya hecho (0.0 to 1.0)
| N.º ejecuciones draw() |
Valores de la variable pct al entrar en la función draw() |
Valores de las variables x e y calculadas dentro del if x = startX + ((stopX-startX) * pct); y = startY + ((stopY-startY) * pct); |
|---|---|---|
| 1 | 0 | x = 20 + ((160 – 20) * 0) ⇒ 0 y = 30 + ((80 – 30) * 0) ⇒ 0 |
| 2 | 0.005 | x = 20 + ((160 – 20) * 0.005) ⇒ 20.7 (21) y = 30 + ((80 – 30) * 0.005) ⇒ 30.25 (30) |
| 3 | 0.010 | x = 20 + ((160 – 20) * 0.010) ⇒ 21.4 (21) y = 30 + ((80 – 30) * 0.010) ⇒ 30.5 (31) |
| 4 | 0.015 | x = 20 + ((160 – 20) * 0.015) ⇒ 22.1 (22) y = 30 + ((80 – 30) * 0.015) ⇒ 30.75 (31) |
Cada posición de x la calculamos sumando a la posición inicial la distancia a recorrer (posición final menos posición inicial), multiplicado por el porcentaje que hemos recorrido.
Como trabajamos en píxeles (y los píxeles no se pueden dividir), el ordenador automáticamente hace un redondeo, que es el valor que hemos puesto entre paréntesis junto al resultado.
Ejercicios
Para entender bien este ejemplo, vale la pena probar a cambiar algunas cosas. Aquí van unas cuantas propuestas:
- Cambiáis el origen y el final. ¿Qué pasa cuando la x del origen (variable startX) es más grande que la x de destino (variable stopX)?
Para entender mejor cómo funciona esto de los pasos, añadiremos una variable más a la que llamaremos numeroP. En esta variable guardaremos el número de pasos que queremos hacer desde el inicio hasta el final. La declaración de variables tendrá que quedar de este modo:
var startX = 20; // Indica la posición x inicial var stopX = 160; // Indica la posición x final var startY = 30; // Indica la posición y inicial var stopY = 80; // Indica la posición y final var numeroP = 200; // Número de pasos a hacer entre los dos puntos. var step = 1.0 / numeroP; // Tamaño de cada paso var pct = 0.0; // Porcentaje ya hecho (0.0 to 1.0)
Con numeroP igual a 200 estamos igual que en el enunciado inicial (step tendrá el valor de 0.005). Cambiad el número de pasos para ver qué cambios se producen.
Movimiento aleatorio
Ya hemos visto cómo la función random() nos permite crear números aleatorios. Como vimos, el primer parámetro que le pasamos es el valor mínimo y el segundo el valor máximo. Con la característica de que el valor máximo no aparecerá nunca. En matemáticas lo expresamos así: [min,max) (el mínimo incluido, el máximo excluido).
Vamos a probar bien la función random(). Probad este código (no necesitamos función setup()):
function draw() {
var r = random(0, 10);
print(r);
}

Este es el resultado: nos escribe números aleatorios entre 0 y 10; 60 por segundo. Son números con muchos decimales.
Demos un paso más, quedémonos solo con la parte entera:
function draw() {
var r = int(random(0, 10));
print(r);
}
Ahora los números que nos da son más comprensibles:
![]()
Demos un paso más, calculando el máximo y el mínimo. Este código os tendría que resultar fácil de entender:
var maxim = 0;
var minim = 99;
function draw() {
var r = int(random(0, 10));
if (r > maxim) {
maxim = r;
print("Nou màxim: ",r);
}
if (r < minim) {
minim = r;
print("Nou mínim: ",r);
}
}
Lo que escribe en la consola este código es algo parecido a esto:
Podemos probar con diferentes números de máximo y mínimo para ver cómo funciona.
Ahora tenemos bastante claro el modo en que funciona la función random(), ahora podemos probar el ejemplo 8-7 del libro. Es muy parecido a nuestro ejemplo, pero pone como máximo la posición x del ratón.
El ejemplo 8-8 es bastante interesante porque genera un efecto muy efectivo. Veamos el código y comentémoslo un poco:
function setup() {
createCanvas(240, 120);
}
function draw() {
background(204);
for (var x = 20; x < width; x += 20) {
var mx = mouseX / 10;
var offsetA = random(-mx, mx);
var offsetB = random(-mx, mx);
line(x + offsetA, 20, x - offsetB, 100);
}
}
Lo que hace este código es, antes que nada, guardar en la variable mx el valor x de la posición del ratón dividido por 10 (divide por 10 para que los cambios sean más suaves). Probad qué pasa si dividimos por 2, por 100 o no dividimos.
La posición del ratón se usa para crear todas las líneas que quepan dentro del canvas, pero separadas 20 píxels entre ellas.
Al pintar cada línea, en la x del inicio y en la x del final les añadimos o restamos un valor calculado aleatoriamente.
El ejemplo 8-9 va un paso más allá y hace todo el movimiento de manera aleatoria. Inicialmente dibuja el círculo en medio del canvas (independientemente del tamaño del canvas) y después el círculo se va moviendo dependiendo de dos valores (uno para x y otro para y) calculados aleatoriamente.
Como siempre, es aconsejable probar el ejemplo y cambiar cosas como por ejemplo el tamaño del canvas (para comprobar que siempre se empieza desde el centro), la velocidad o el diámetro del círculo.
Temporizadores
p5.js cuenta el tiempo desde que se inicia la ejecución de nuestro programa. Nosotros podemos consultar el tiempo pasado desde el inicio mediante la función millis(). El ejemplo 8-10 nos permite ver cómo va pasando el tiempo. La función millis() nos devuelve el tiempo en milisegundos, lo que quiere decir que 1000 ⇒ 1 segundo.
El uso de la función millis() nos permite hacer que en nuestro programa pasen cosas en un momento determinado. El ejemplo 8-11 es un caso de ello. A continuación, tenéis otro ejemplo que comentaremos paso a paso. Básicamente, es un círculo que se hace más grande cada segundo, hasta que llega a un diámetro de 200. A partir de este momento se va haciendo más pequeño cada vez, hasta llegar a un diámetro de 0 que vuelve a crecer.
var diametro = 0;
var crece = true; // Variable que determina si el círculo tiene que
// crecer o decrecer
function setup() {
createCanvas(480, 480);
}
function draw() {
var currentTime = millis(); // Guardamos el tiempo actual
background(204);
if (currentTime % 1000 > 900) { // Calculamos el residuo de dividir
// por 1000
if (diametro == 200) { // Si llegamos a 200 toca decrecer
crece = false;
}
if (diametro == 0) { // Si llegamos a 0 volver a crecer
crece = true;
}
if (crece) {
diametro++;
} else {
diametro--;
}
}
ellipse(width/2, height/2, diametro, diametro);
}
Este ejemplo es muy sencillo y es fácil ver cómo funciona. La única dificultad está en el hecho de usar el residuo de la división por 1000.
Movimiento circular
Vamos a ver cómo hacer mover objetos por el canvas, usando un movimiento circular. Para hacerlo, usaremos las funciones sen() y cos() que corresponden al seno y al coseno. Como no podemos explicar trigonometría aquí, nos tendremos que conformar sabiendo que estas funciones devuelven valores de entre -1 y 1.
Aquí tenéis un ejemplo que nos permite hacernos una idea de cómo podemos usar las funciones senos y cosenos:
var x = 0.0;
function setup() {
createCanvas(400, 400);
strokeWeight(4);
}
function draw() {
stroke(0);
point(x*10,sin(x)*50+200);
stroke(255,0,0)
point(x*10,cos(x)*50+200);
x=x+0.08;
}
Este código da como resultado este dibujo:
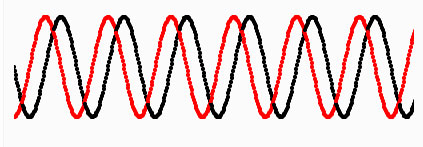
Donde la función seno se ha dibujado en negro y la coseno en rojo.
Pues bien, estas dos funciones se pueden usar para varias cosas. Por ejemplo, en el ejemplo 8-12 se usa para generar una sensación de oscurecimiento y aclaración del color del cuadro. En este código se usa la función map() que, recordaréis, nos permite hacer un cambio de escala de un valor. Así, como la funció sen() devuelve un valor que va desde -1 hasta 1 y se quiere tener un número que vaya desde 0 (negro) hasta 255 (blanco), queremos convertir el resultado de calcular el seno en un color.
var sinval = sin(angle); print(sinval); var gray = map(sinval, -1, 1, 0, 255); background(gray);
El ejemplo 8-13 nos muestra cómo se puede usar la función sen()para generar movimiento.
Combinando la función sen() y la función cos() para dar valor a x e y, podemos hacer movimientos circulares. El ejemplo 8-14 aprovecha esta posibilidad. Modificamos y comentamos el ejemplo del libro.
var angle = 0.0;
var offset = 120; // El centro del movimiento circular.
// x = 120 i y = 120 es el centro del canvas.
var scalar = 50; // Un valor más grande dibuja un círculo más grande
var speed = 0.05;
function setup() {
createCanvas(240, 240);
background(204);
}
function draw() {
var x = offset + cos(angle) * scalar;
var y = offset + sin(angle) * scalar;
ellipse(x, y, 40, 40);
angle += speed;
}
El último ejemplo de este capítulo es el 8-15, que no es complicado. Este dibuja una espiral. El punto clave está en la variable scalar, que cambia en cada vuelta y multiplica el resultado del seno y coseno.